Co przedstawia karta kontrolna?

Karta kontrolna jest narzędziem wykorzystywanym w procesie zarządzania jakością. Jest to wykres lub tabela służąca do monitorowania i kontrolowania procesu, jakości produktu lub usługi. Karta kontrolna jest używana do określenia, czy dane wyniki lub wskaźniki są w normie, czy też należy podjąć działania naprawcze. Karta kontrolna może być wykorzystywana również do ustalenia, czy nastąpiła poprawa jakości produktu.

Karty kontrolne , znane również jako karty Shewharta (twórca: Walter A. Shewhart) lub karty kontrolne procesu , są statystycznym narzędziem kontroli procesu stosowanym do ustalenia, czy proces produkcyjny lub biznesowy jest w stanie kontroli. Bardziej właściwe jest stwierdzenie, że karty kontrolne są urządzeniem graficznym do statystycznego monitorowania procesów.

Zaufali mi najlepsi:

MEGA SKUTECZNY KURS, dzięki któremu nauczysz się pisać reklamy i zwiększysz zyski.

Kliknij w obrazek poniżej:

Zadaniem organizacji jest zapewnienie warunków, aby odchylenia były jak najmniejsze oraz aby miały charakter naturalny.

Karta kontrolna zawsze ma środkową linię dla średniej, górną linię dla górnej granicy kontroli i dolną linię dla dolnej granicy kontroli. Linie te są określane na podstawie danych historycznych.

Porównując bieżące dane z tymi liniami, można wyciągnąć wnioski dotyczące tego, czy zmiana procesu jest spójna (pod kontrolą), czy nieprzewidywalna (poza kontrolą, na którą wpływ mają specjalne przyczyny zmienności).

To wszechstronne narzędzie do gromadzenia i analizy danych może być wykorzystywane przez różne branże i jest uważane za jedno z siedmiu podstawowych narzędzi jakości.

Karta kontrolna – budowa

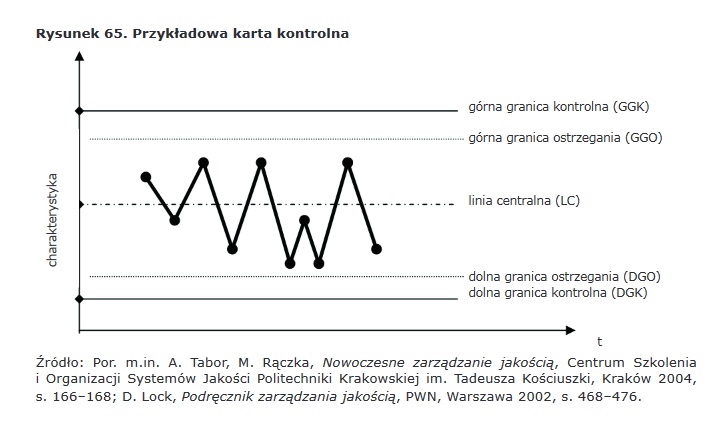
Karta kontrolna jest wykresem używanym do badania zmian procesu w czasie. Dane są wykreślane w kolejności czasowej.

Na osi X karty kontrolnej odkłada się numer próby (oraz czas). Natomiast oś Y zawiera badane wielkości statystyczne (w zależności od rodzaju karty), np. wartości średnie, rozstępy lub inne. Linia centralna (LC) odpowiada nominalnej wartości analizowanej zmiennej – odzwierciedla średni przebieg procesu. Dolna i górna granica ostrzegania (DGO i GGO) nazywane są czasami granicami akcji. Ich przekroczenie nie oznacza jesz-cze rozregulowania procesu, ale może być ostrzeżeniem o zbliżającym się problemie. Dolna i górna granica kontrolna (DGK i GGK) to linie, których przekroczenie oznacza, że proces jest rozregulowany i konieczna jest ingerencja w proces(źródło).

REKLAMA

Koniecznie zobacz NAJLEPSZE szkolenie z Facebooka na rynku

Link do kursu: szkolenie Facebook Ads

Koniec reklamy.

Podstawowa procedura

1. Wybierz odpowiedni wykres kontrolny dla swoich danych.
2. Określ odpowiedni czas na zebranie i wykreślenie danych.
3. Zbieraj dane, konstruuj wykres i analizuj dane.
4. Poszukaj „sygnałów poza normą” na karcie kontrolnej. Kiedy któryś zostanie zidentyfikowany, zaznacz go na wykresie i zbadaj przyczynę. Dokumentuj, w jaki sposób badałeś, czego się nauczyłeś, przyczynę i jak to naprawiono.
5. Kontynuuj sprawdzanie danych w miarę ich generowania. Po wykreśleniu każdego nowego punktu danych sprawdź, czy nie ma nowych sygnałów poza normą.
6. Po uruchomieniu nowej karty kontrolnej proces może być poza kontrolą. Jeśli tak, limity kontrolne obliczone na podstawie pierwszych 20 punktów są limitami warunkowymi. Jeśli masz co najmniej 20 kolejnych punktów z okresu, w którym proces działa pod kontrolą, ponownie oblicz granice kontroli.

Interpretowanie kart kontrolnych

Sukces używania kart kontrolnych w dużej mierze zależy od prawidłowej interpretacji otrzymanych wykresów.

Żeby stwierdzić, że analizowany proces jest pod kontrolą, muszą być spełnione niżej wymienione warunki:

1. Absolutnie wszystkie punkty muszą się mieścić między górną i dolną linią kontrolną,
2. Większość punktów musi znajdować się bliżej linii centralnej niż granic kontrolnych,
3. Punkty nie mogą wykazywać trendów ani cykli świadczących o nienaturalnych przyczynach zmienności,
4. Punkty nie mogą tworzyć powtarzających się okresowo wzorców i układów,
5. Liczba punktów znajdujących się powyżej lub poniżej linii centralnej musi być w przybliżeniu jednakowa,
6. Linie łączące poszczególne punkty na wykresie powinny przecinać linię centralną.

Jeśli zauważysz, że wykres przyjmuje właściwości które wymienię za chwilę to możesz stwierdzić, że zachowuje się w sposób niekontrolowany:

• punkt (punkty) na karcie wypadają poza dolną lub górną granicę kontrolną,
• dwa z trzech kolejnych punktów leżą bardzo blisko górnej lub dolnej linii kontrolnej,
• seria dziewięciu kolejnych punktów leży po jednej stronie linii centralnej,
• szereg sześciu punktów leży wzdłuż prostej rosnącej lub malejącej,
• czternaście kolejnych punktów na przemian rosnących i malejących,
• cztery z pięciu kolejnych punktów leżą w strefie między linią ostrzegania i kontrolną,
• piętnaście kolejnych punktów oscyluje wokół linii centralnej,
• osiem kolejnych punktów leży po obu stronach linii centralnej, ale żaden z nich w jej pobliżu.

Zastosowanie kart kontrolnych. Kiedy stosować karty kontrolne?

1. Podczas przewidywania oczekiwanego zakresu wyników procesu
2. Do określania, czy w danym momencie proces jest pod kontrolą, czy nie.
3. Do analizowania odchyleń w stabilności procesu pod wpływem czynników naturalnych i szczególnych.
4. W celu zidentyfikowania obszarów możliwego doskonalenia.
5. W celu sprawowania bieżącej kontroli nad procesem – odnajdywania i usuwania po-wstających problemów.
6. W celu oceny efektywności wprowadzonych zmian.
7. W celu zapobiegania produkcji wyrobów wadliwych.
8. W celu prognozowania przyszłego zachowania się procesu. Podczas kontrolowania bieżących procesów poprzez znajdowanie i korygowanie pojawiających się problemów
9. Do oceny stabilności procesu w długich okresach.
10. Podczas określania, czy proces jest stabilny (w kontroli statystycznej)
11. Podczas analizy wzorców zmienności procesu ze specjalnych przyczyn (zdarzenia nietypowe) lub wspólnych przyczyn (wbudowanych w proces)
12. Podczas określania, czy projekt poprawy jakości powinien mieć na celu zapobieganie konkretnym problemom lub wprowadzenie zasadniczych zmian w procesie 

Rodzaje kart kontrolnych

Karty kontrolne są często klasyfikowane według charakterystyk jakości, które monitorują. Istnieją karty kontrolne przy ocenie liczbowej (inaczej nazywane kartami cech mierzalnych) i przy ocenie alternatywnej (inaczej nazywane kartami cech alternatywnych).

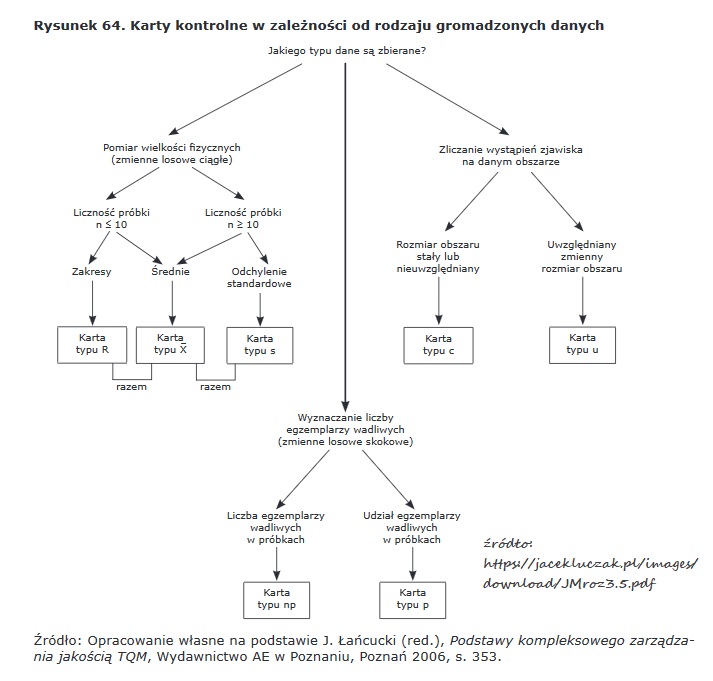
Ocena liczbowa

Karty pojedynczych obserwacji (xi). Karta pojedynczych obserwacji służy do nadzorowania nieprzetworzonych wyników pomiarów. Jest stosowana w przypadkach gdy wykonanie próby kilkuelementowej nie jest możliwe ze względów technicznych lub nieuzasadnione ze względów ekonomicznych.

Karta ruchomego rozstępu ® , różnic, R – karta Shewharta ruchomego rozstępu R (analizy pojedyncze),

Karta mediany i rozstępu Me – R. Karty te swoim charakterem przypominają w dużym stopniu karty X – Rśr oraz X – σ. Są bardzo łatwe w użyciu, jednak charakteryzują się mniejszą dokładnością pomiarów.

Karta akceptacji procesu nazywana również kartą odbiorczą, służy do nadzorowania ryzyka wynikającego z rozregulowania procesu. Przy projektowaniu karty akceptowana jest frakcja braków.

Karta ruchomej średniej MA (ang.Moving Average) służy głównie,podobnie jak karta CUSUM, do wykrywania małych przesunięć wartości średniej procesu oraz pojawiających się trendów. Istota prowadzenia karty ruchomej średniej polega na tym, że „wartość” wykreślanych punktów nie jest bezpośrednio wartością zmierzoną lub średnią w danej próbce, ale wartością średnią z kilku ostatnich próbek. Jako jeden z parametrów ustawia się tu bowiem tzw. szerokość okna, tzn. podaje z jakiej liczby ostatnich próbek będzie liczona średnia do wyznaczenia położenia wykreślanego punktu.

Karta wartości średniej (X-średnie). Na tej karcie wykreślane są średnie z próbki, aby monitorować średnie wartości zmiennej obserwowanej (np. rozmiar pierścieni tłokowych, wytrzymałość materiału itd.). Służy do badania zdolności procesu do wyprodukowania wyrobu o akceptowalnej jakości. Poprzez losowe pobranie próbek można stwierdzić, czy proces jest stabilny. Karta ta z reguły jest łączona z kartą kontrolną rozstępu (Rśr).

Karta kontrolna Rśr. Na tej karcie wykreślane są wartości rozstępu z próbki, otrzymywane w rezultacie kolejnych badań zmienności obserwowanej zmiennej. Stosowanie wyłącznie karty kontrolnej X nie jest w pełni efektywne, dlatego że mówi ona jedynie o dokładności procesu. Natomiast drugą, bardzo ważną cechą każdego procesu jest precyzja obrazowana właśnie przez kartę Rśr, dlatego właśnie zasadne jest łączenie tych kart. Karta Rśr umożliwia zaobserwowanie różnic między największą a najmniejszą obserwacją w próbie

Karta σ (odchylenia standardowego). Na tej karcie wykreślane są wartości odchylenia standardowego z próbki, otrzymywane w rezultacie kolejnych badań zmienności obserwowanej zmiennej. Jest to karta o podobnych właściwościach do karty Rśr, jednak ma większą zdolność do wykrywania zmian zachodzących w procesie

Karta S². Na tej karcie wykreślane są wartości wariancji z próbki, otrzymywane w rezultacie kolejnych badań zmienności obserwowanej zmiennej.

Karta sum skumulowanych (CU-SUM). Karta kontrolna stosowana do wewnętrznej kontroli jakości badań w laboratorium (tj. kontroli pomiarów, analiz, procesów technologicznych). Stanowi ona często dopełnienie karty średniej.

Karta CuSum jest oparta na różnicach między wartościami średnimi, pobieranych w regularnych odstępach czasu serii, a wartością odniesienia. Serie (próbki) składające się z n pomiarów są pobierane systematycznie (np. raz na dzień lub raz na tydzień).
Wartość, która jest umieszczana na wykresie, obliczana jest ze wzoru:

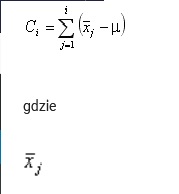
jest średnią z n pomiarów dla j-tej próbki, µ jest wartością odniesienia, a i jest numerem wprowadzanej na wykres próbki (i = 1, …, m).

Jeżeli proces wykonywania analiz jest poprawny, oczekuje się, że punkty naniesione na kartę CuSum będą układały się wokół zera wzdłuż osi poziomej (nr próbki).

Jeżeli punkty naniesione na wykres zaczną tworzyć linię nachyloną względem osi poziomej, oznacza to, że pojawia się błąd systematyczny i trzeba analizy wykonywane daną metodą wstrzymać do rozwiązania problemu.

Analiza tej karty opiera się na trzech zasadach:

1. średnia procesu jest bliska przyjętej nominalnej wartości, jeśli wartości skumulowane znajdują się blisko linii poziomej,
2. średnia procesu jest mniejsza od przyjętej nominalnej wartości, jeśli wartości skumulowane tworzą trend o nachyleniu w dół,
3. średnia procesu jest większa od przyjętej nominalnej wartości, jeśli wartości skumulowane tworzą trend o nachyleniu w górę.

Ocena alternatywna

Karty kontrolne przy ocenie alternatywnej stosuje się w przypadku, gdy sterowanie procesem odbywa się dzięki analizie tzw. alternatywnych danych. Dane te to po prostu informacje o postaci:

• wyrób dobry/wyrób zły,
• dana cecha występuje/ nie występuje,
• usterka występuje/nie występuje itp.

Mamy więc do czynienia z tzw. zmienną zero jedynkową.

Karta P. Na tej karcie wykreśla się frakcję (procent) jednostek (elementów) wadliwych (niezgodnych) w próbkach produktu (podobnie jak na karcie U). Jednakże granice kontrolne nie są tu oparte na rozkładzie rzadkich zdarzeń lecz na rozkładzie dwumianowym. Dlatego też karta ta ma zastosowanie w sytuacjach, gdy pojawianie się braków nie jest rzadkie (np. jeśli oczekiwany procent braków jest większy niż 5% ogólnej liczby produkowanych sztuk).

Karta U. Na tej karcie wykreśla się wskaźnik liczby wad, niezgodności, obliczany jako stosunek liczby wad do liczby badanych jednostek (liczność-n; np. długość rury, liczba partii towaru). W przeciwieństwie do karty C, ta karta nie wymaga stałej liczby badanych jednostek i może być stosowana wówczas, gdy na przykład partie (próbki) mają różną liczność.

Karta Np. Na tej karcie wykreśla się liczbę jednostek (elementów) wadliwych (niezgodnych) w próbkach o stałej liczności (podobnie jak na karcie C). Jednakże granice kontrolne nie są tu oparte na rozkładzie rzadkich zdarzeń, lecz na rozkładzie dwumianowym. Dlatego karta ta powinna być używana, gdy pojawianie się wad nie jest rzadkością (np. wady pojawiają się w więcej niż 5% badanych jednostek). Na przykład, można stosować tę kartę do kontrolowania produktów z wadami drugorzędnymi.

Karta C. Na tej karcie wykreśla się liczbę wad, niezgodności (na partię, na dzień, na maszynę, na 100 metrów długości rury itd.). W przypadku tej karty przyjmuje się, że wady jakościowe są zdarzeniami rzadkimi i granice kontrolne na tej karcie wyznaczane są na podstawie rozkładu Poissona (rozkład zdarzeń rzadkich).

Karty kontrolne Excel

Oto link do karty kontrolnej w excelu na moim dysku Google. Wystarczy że ją ściągniesz do siebie i możesz swobodnie edytować:

Karta kontrolna excel https://drive.google.com/file/d/1LRYD1Xt5a6ymzg5pfZEiC_gepMNYtUJ8/view?usp=sharing

A wygląda to mniej więcej tak:

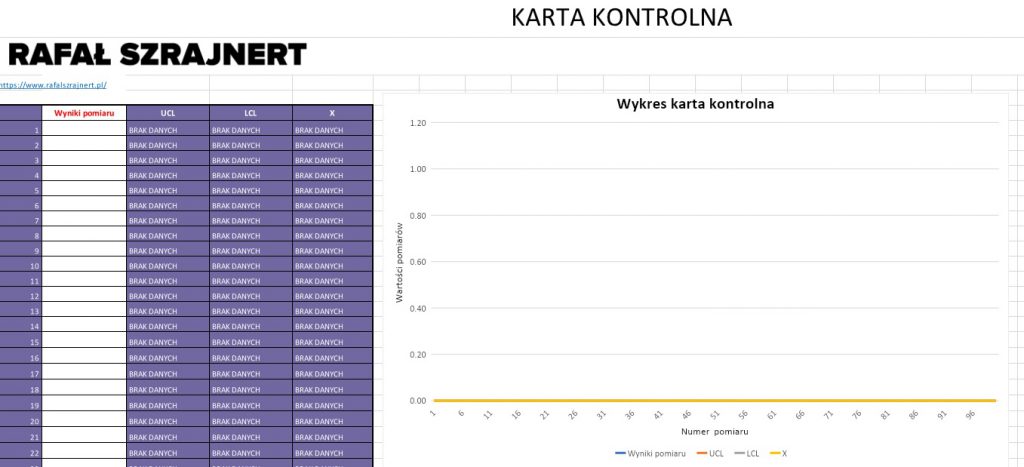
Przykładowy arkusz Excel do ściągnięcia (wersja angielska):

https://asq.org/-/media/public/learn-about-quality/data-collection-analysis-tools/asq-control-chart.xls?la=en

A poniżej film, jak stworzyć własną kartę kontrolną w Excelu:

• szkolenia online
• szkolenia u Ciebie w firmie i doradztwo-konsulting
• agencja SEO/SEM

Co myślisz o moim nowym wpisie na blogu?

A może masz pytanie dotyczące strategii lub techniki jak działać najlepiej?

Tak czy inaczej, chciałbym usłyszeć, co masz do powiedzenia.

Więc śmiało, teraz udostępnij ten wpis na swoich social mediach i zobacz co inni mają do powiedzenia.