Co to jest błąd koniunkcji? Definicja.

Błąd koniunkcji (ang. conjunction fallacy), należący do grupy heurystyki reprezentatywności, jest częstym błędem rozumowania, w którym uważamy, że dwa zdarzenia zachodzące w połączeniu są bardziej prawdopodobne niż jedno z tych wydarzeń, które zachodzi samodzielnie.

Oto dlaczego tak się dzieje i jak możemy przezwyciężyć błąd koniunkcji.

Daniel Kahneman i Amos Tversky spędzili dziesięciolecia na badaniach psychologicznych, aby rozwikłać wzorce błędów ludzkiego rozumowania. Odkryli szereg błędów logicznych, które zwykle popełniamy, mając do czynienia z informacjami, które wydają się niejasno znajome. Te błędy prowadzą do uprzedzeń – irracjonalnych zachowań opartych na przekonaniach, które nie zawsze są zakorzenione w rzeczywistości.

W swojej książce Thinking Fast and Slow, która podsumowuje pracę jego i Tversky’ego, Kahneman wprowadza uprzedzenia wynikające z błędu koniunkcji – fałszywego przekonania, że koniunkcja dwóch wydarzeń jest bardziej prawdopodobna niż jedno zdarzenie samo w sobie.

Błąd koniunkcji co to? Definicja i prosty przykład (sławna Linda)

Błąd koniunkcji definicja i przykład:

Najczęściej cytowany przykład tego błędu pochodzi od Tversky’ego i Kahnemana. Chociaż opis i osoba przedstawiana są fikcyjne, sekretarka Amosa Tversky’ego w Stanford nazywał się Linda Covington i nazwał jej imieniem właśnie słynny przykład, który wyjaśnia czym jest błąd koniunkcji- („problem Lindy”, ang. Linda problem)

Linda ma 31 lat, jest stanu wolnego, szczera i bardzo inteligentna. Ukończyła filozofię. Jako studentka głęboko zajmowała się problematyką dyskryminacji i sprawiedliwości społecznej, a także brała udział w demonstracjach antynuklearnych.

Co jest bardziej prawdopodobne?

Linda jest kasjerką w banku.
Linda jest kasjerką w banku i jest aktywna w ruchu feministycznym.

Większość pytanych wybrała opcję 2. Jednak prawdopodobieństwo wystąpienia dwóch zdarzeń razem (w „koniunkcji”) jest zawsze mniejsze lub równe prawdopodobieństwu wystąpienia jednego z nich samodzielnie – formalnie dla dwóch zdarzeń A i B ta nierówność może być napisana jako:

Można to łatwo policzyć i udowodnić błąd koniunkcji.

Na przykład, nawet wybierając bardzo niskie prawdopodobieństwo, że Linda będzie kasjerką, powiedzmy Pr (Linda jest kasjerką) = 0,05 i wysokie prawdopodobieństwo, że będzie feministką, powiedzmy Pr (Linda jest feministką) = 0,95, a następnie zakładając niezależność, Pr (Linda jest kasjerką bankową, a Linda jest feministką) = 0,05 × 0,95 lub 0,0475, mniej niż Pr (Linda jest kasjerką).

Widzicie wyniki? 0,05 kontra 0,0475 nawet przy ułożeniu prawdopodobieństw na korzyść opcji B, ta opcja zawsze przegrywa.

Tversky i Kahneman twierdzą, że większość ludzi źle rozumie ten problem, ponieważ używa heurystycznej (łatwej do obliczenia) procedury zwanej reprezentatywnością, aby dokonać tego rodzaju osądu: Opcja 2 wydaje się bardziej „reprezentatywna” dla Lindy na podstawie jej opisu, mimo, że jest to wyraźnie mniej prawdopodobne matematycznie.

W innych demonstracjach argumentowali, że konkretny scenariusz wydaje się bardziej prawdopodobny ze względu na reprezentatywność, ale każdy dodany szczegół faktycznie sprawi, że scenariusz będzie coraz mniej prawdopodobny.

Co to jest prawdopodobieństwo?

Prawdopodobieństwo może być trudną koncepcją. Ale jest bardzo pomocne przy rozumieniu co błąd koniunkcji powoduje.

Większość z nas intuicyjnie rozumie, czym jest prawdopodobieństwo, ale nie ma zgody co do tego, co to w rzeczywistości oznacza. Jest to tak samo niejasne i subiektywne pojęcie jak demokracja, piękno czy wolność. Nie zawsze jest to jednak kłopotliwe – nadal możemy spokojnie omówić to zagadnienie.

Chociaż statystycy mogą się nie zgodzić, dla większości z nas prawdopodobieństwo jest po prostu narzędziem opisującym stopień naszej wiary, że coś się wydarzy lub nie. Na przykład wiemy, że jutro wzejdzie słońce i uważamy za prawie niemożliwe jest, aby wieczorem na niebie pojawiły się 2 księżyce. Oprócz skrajności istnieją również zdarzenia, które znajdują się gdzieś pośrodku spektrum prawdopodobieństwa, takie jak stopień przekonania, że ​​jutro będzie padać.

Pomimo swojej niejasności prawdopodobieństwo ma swoje zalety. Przypisywanie prawdopodobieństw pomaga nam uczynić stopień przekonania wykonalnym, a także możemy przekazać innym wartościowe wskazówki.

Jeśli uważamy, że prawdopodobieństwo, że jutro będzie padał deszcz, wynosi 90%, prawdopodobnie będziemy nosić parasolkę i zasugerujemy, aby zrobiła to również nasza rodzina.

Prawdopodobieństwo, wartość bazowa i reprezentatywność

Większość z nas jest już zaznajomiona z reprezentatywnością i wartościami bazowymi. Rozważmy klasyczny przykład x liczby czarnych i y liczby białych kulek w słoiku.

Jest to prostym ćwiczeniem, aby powiedzieć, jakie są prawdopodobieństwa wylosowania każdego koloru, jeśli znasz ich wartości bazowe (proporcje).

Jeśli np w słoiku 90% kulek jest koloru czarnego, a 10% koloru białego to bez problemu obliczysz prawdopodobieństwo wylosowania danego koloru.

Stosowanie wartości bazowych jest oczywistym podejściem do szacunków, gdy nie są dostarczane żadne inne informacje.

Jednak Kahnemanowi udało się udowodnić, że w świetle konkretnych opisów mamy tendencję do ignorowania wartości bazowych. Nazywa to zjawisko nastawieniem reprezentatywnym.

Aby zilustrować stronniczość reprezentatywności, weźmy pod uwagę przykład osoby czytającej gazetę Newsweek albo Forbes w warszawskim metrze. Jak myślisz, co byłoby lepsze aby scharakteryzować nieznajomego czytelnika?

1) Ma tytuł doktora.
2) Nie ma wykształcenia wyższego.

Reprezentatywność podpowiadałaby, że warto postawić na stopień doktora, ale niekoniecznie jest to dobry pomysł. Powinieneś poważnie rozważyć drugą alternatywę, ponieważ w warszawskim metrze jeździ znacznie więcej studentów niż doktorantów, czy osób już posiadających ten tytuł.

Podczas gdy większa część doktorów może czytać wymienione przeze mnie gazety, całkowita ich liczba czytelników, którzy mają niższe stopnie naukowe (lub wcale ich nie posiadają), prawdopodobnie będzie znacznie większa, nawet jeśli sam odsetek jest bardzo niewielki.

W serii podobnych eksperymentów badani Kahnemana nie rozpoznali podstawowych wskaźników w świetle indywidualnych informacji. To nie jest zaskakujące.

Kahneman wyjaśnia, że w większości przypadków ludzie, którzy zachowują się przyjaźnie, są w rzeczywistości przyjaźni. Bardzo wysoki i szczupły sportowiec znacznie częściej gra w koszykówkę niż w piłkę nożną. Osoby ze stopniem doktora częściej kupują prenumeratę Harvard Business Review niż osoby, które zakończyły edukację po ukończeniu szkoły średniej. Młodzi mężczyźni częściej niż starsze kobiety jeżdżą szybko autem.

Chociaż przestrzeganie błędu reprezentatywności może poprawić ogólną dokładność, nie zawsze będzie to statystycznie optymalne podejście.

W swoim bestsellerze Moneyball Michael Lewis opowiada historię trenera drużyny baseballowej, który rozpoznał ten błąd i wykorzystał go na swoją korzyść.

Książka stała się tak popularna, że nakręcono na ten temat nawet film z Bradem Pittem:

Podczas rekrutacji nowych graczy do zespołu, zamiast polegać na opiniach, trener polegał głównie na statystykach poprzednich wyników. Takie podejście pozwoliło mu zbudować zespół świetnych graczy, których pomijały inne zespoły. Nie trzeba dodawać, że zespół osiągnął doskonałe wyniki przy niewielkich kosztach.

Heurystyki reprezentatywności. Omówmy błąd koniunkcji jeszcze raz mając powyższe informacje

Wyjaśniając prawdopodobieństwo, wartość bazową i reprezentatywność zyskaliśmy owy wgląd w błąd koniunkcji. Teraz możemy wejść jeszcze bardziej w szczegóły zagadnienia.

Podczas gdy błąd reprezentatywności występuje, gdy nie uwzględniamy niskich wartości bazowych, błąd koniunkcji pojawia się, gdy przypisujemy większe prawdopodobieństwo zdarzeniu o wyższej specyficzności. To narusza prawa prawdopodobieństwa.

Rozważ następujące badanie:

Uczestnicy zostali poproszeni o uszeregowanie czterech możliwych wyników następnego turnieju Wimbledonu od najbardziej do najmniej prawdopodobnego. Björn Borg był dominującym tenisistą w dniu, w którym przeprowadzono badanie. Oto wyniki:

A. Borg wygra mecz.
B. Borg przegra pierwszego seta.
C. Borg przegra pierwszego seta, ale wygra mecz.
D. Borg wygra pierwszego seta, ale przegra mecz.

Jak Ty byś obstawił?

Kahneman był zaskoczony, widząc, że większość badanych uporządkowała szanse, bezpośrednio zaprzeczając prawom logiki i prawdopodobieństwa.

Krytyczne pozycje to B i C. B jest zdarzeniem bardziej wszechstronnym i jego prawdopodobieństwo musi być wyższe niż zdarzenia, które obejmuje. Wbrew logice, ale nie reprezentatywności lub wiarygodności, 72% przypisało B niższe prawdopodobieństwo niż C.

Jeśli dokładnie przemyślałeś problem, narysowałeś w głowie następujący diagram.

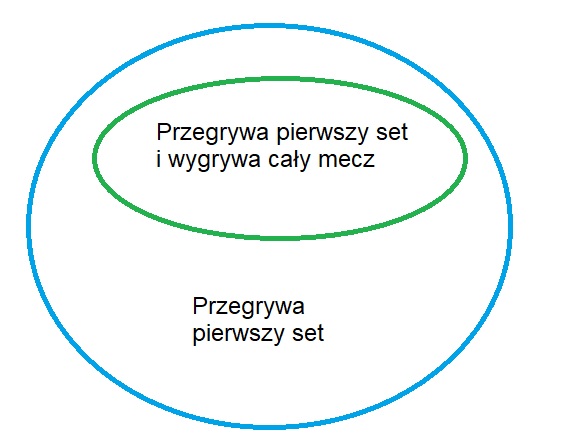
Przegrana pierwszego seta z definicji zawsze będzie bardziej prawdopodobnym zdarzeniem niż przegrana pierwszego seta i wygrana w meczu.

REKLAMA

Koniecznie zobacz NAJLEPSZE szkolenie z Facebooka na rynku

Link do kursu: szkolenie Facebook Ads

Koniec reklamy.

Rola wiarygodności

Błąd reprezentatywności i koniunkcji pojawia się, ponieważ dokonujemy mentalnego skrótu od naszej postrzeganej wiarygodności scenariusza do jego prawdopodobieństwa.

Najbardziej spójne historie niekoniecznie są najbardziej prawdopodobne, ale są wiarygodne, a pojęcia spójności, prawdopodobieństwa i wiarygodności są łatwo mylone.

Reprezentatywność należy do grupy blisko powiązanych ocen, które prawdopodobnie zostaną wygenerowane razem. Najbardziej reprezentatywne wyniki łączą się z opisem osobowości, tworząc najbardziej spójne historie.

Kahneman ostrzega nas przed skutkami tych uprzedzeń na nasze postrzeganie opinii ekspertów i prognoz. Wyjaśnia, że ​​jesteśmy bardziej skłonni uwierzyć w scenariusze, które są raczej ilustracyjne niż prawdopodobne.

Bezkrytyczne zastępowanie prawdopodobieństwa wiarygodnością ma zgubny wpływ na sądy, gdy scenariusze są używane jako narzędzia prognozowania.

Rozważ te dwa scenariusze, które zostały przedstawione różnym grupom, z prośbą o ocenę ich prawdopodobieństwa:

• Ogromna powódź gdzieś w Ameryce Północnej w przyszłym roku, w której utonie ponad 1000 osób
• Trzęsienie ziemi w Kalifornii w przyszłym roku, powodujące powódź, w której utonie ponad 1000 osób

Scenariusz trzęsienia ziemi w Kalifornii jest bardziej prawdopodobny niż scenariusz dla Ameryki Północnej, chociaż jego prawdopodobieństwo jest z pewnością mniejsze. Zgodnie z oczekiwaniami, oceny prawdopodobieństwa były wyższe w przypadku bogatszego i bardziej szczegółowego scenariusza, wbrew logice.

To pułapka dla prognostów, analityków i ich klientów: dodawanie szczegółów do scenariuszy sprawia, że ​​są one bardziej przekonujące, ale mniej prawdopodobne, że się spełnią.

Jak sobie z tym radzić?

Pierwsza lekcja jasnego myślenia to pytanie, jak myślisz. Nie powinniśmy po prostu wierzyć we wszystko, co przyjdzie nam do głowy – nasze przekonania muszą być ograniczone logiką.

Nie musisz być ekspertem w zakresie prawdopodobieństwa, aby oswoić swoją intuicję, ale znajomość prostych pojęć pomoże. Istnieją dwie główne zasady, które warto powtórzyć w świetle nastawienia na reprezentatywność:

1) Wszystkie prawdopodobieństwa sumują się do 100%.

Oznacza to, że jeśli uważasz, że jutro będzie padać deszcz z 90% prawdopodobieństwem, to jest 10% szans, że jutro nie będzie padać.

Ponieważ jednak wierzysz, że jutro będzie padać deszcz, jest tylko 90% szans, więc nie możesz mieć 95% pewności, że jutro rano będzie padać.

Zwykle popełniamy tego typu błąd, kiedy mówimy, że jeśli pada deszcz, istnieje 95% prawdopodobieństwo, że stanie się to rano. To inne twierdzenie, a prawdopodobieństwo wystąpienia deszczu jutro rano wynosi 0,9 * 0,95 = 85,5%.

Oznacza to również, że jeśli pada deszcz, to nie będzie padać rano, wynosi 90,0% -85,5% = 4,5%.

2) Druga zasada to Twierdzenie Bayesa.

Pozwala nam poprawnie dostosować nasze przekonania do diagnostyki dowodów. Reguła Bayesa jest zgodna ze wzorem:

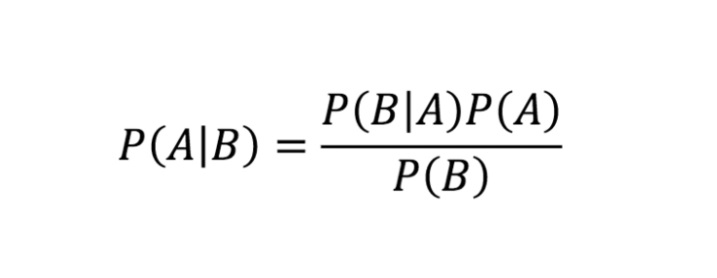
gdzie A i B są zdarzeniami oraz P(B)>0, przy czym:

• P(A|B) oznacza prawdopodobieństwo warunkowe, tj. prawdopodobieństwo zajścia zdarzenia A, o ile zajdzie zdarzenie B.
• P(B|A) oznacza prawdopodobieństwo zajścia zdarzenia B, o ile zajdzie zdarzenie A.

Zasadniczo wzór stwierdza, że ​​późniejsze szanse są proporcjonalne do poprzednich pomnożonych przez prawdopodobieństwo.

Kahneman krystalizuje dwa klucze do zdyscyplinowanego rozumowania bayesowskiego:

• Oprzyj swoją ocenę prawdopodobieństwa wyniku na wiarygodnej wartości bazowej.
• Kwestionuj diagnostyczność swoich dowodów.

Kahneman wyjaśnia to na przykładzie:

Jeśli uważasz, że 3% absolwentów jest zapisanych na informatykę (wartość bazowa), a także uważasz, że opis Tomasza jest 4 razy bardziej prawdopodobny dla absolwenta informatyki niż na innych kierunkach, to reguła Bayesa mówi: musisz uwierzyć, że prawdopodobieństwo, że Tomek jest studentem informatyki, wynosi teraz 11%.

Cztery razy większe prawdopodobieństwo oznacza, że ​​spodziewamy się, że około 80% wszystkich studentów informatyki będzie przypominać Tomasza.

Używamy tej proporcji do uzyskania skorygowanych kursów.

Obliczenie wygląda następująco: 0,03 * 0,8 / (0,03 * 0,8 + ((1-0,03) * (1-0,8))) = 11%

Najłatwiejszym sposobem, aby stać się lepszym w podejmowaniu decyzji, jest kwestionowanie swoich założeń i postępowanie zgodnie z mocnymi dowodami. Gdy dowody są niepotwierdzone, dostosuj je minimalnie i zaufaj wartościom bazowym. Prawdopodobnie będziesz mile zaskoczony.

Ciekawostka

Zwracanie uwagi na ustalone relacje, używanie częstotliwości zamiast prawdopodobieństwa i / lub myślenie diagramowe ostro redukuje błąd w niektórych formach błędu koniunkcji.

W jednym eksperymencie kwestia problemu Lindy została przeformułowana w następujący sposób:

Jest 100 osób, które pasują do powyższego opisu (czyli Lindy). Ile z nich jest:

• Kasjerem w banku? _ z 100
• Kasjerem w banku i działa w ruchu feministycznym? _ z 100

Podczas gdy wcześniej 85% uczestników udzieliło złej odpowiedzi (kasjerka i aktywna w ruchu feministycznym), w eksperymentach przeprowadzonych z tym pytaniem żaden z uczestników nie podał złej odpowiedzi.

Uczestnicy zostali zmuszeni do zastosowania podejścia matematycznego, dzięki czemu łatwiej rozpoznali różnicę.

Jednak w niektórych zadaniach opartych wyłącznie na częstotliwościach, a nie na opowieściach, które wykorzystywały jasne, logiczne sformułowania, błędy koniunkcji nadal występowały dominująco, gdy obserwowany wzorzec częstotliwości przypominał koniunkcję.

Model mentalny

Model mentalny to wyjaśnienie procesu myślowego o tym, jak coś działa w prawdziwym świecie. Jest reprezentacją otaczającego świata, relacji między jego różnymi częściami oraz intuicyjnego postrzegania przez człowieka własnych czynów i ich konsekwencji

Zrozumienie tego jest ścieżką prowadzącą do podejmowania najlepszych decyzji.

Zachęcam do podzielenia się swoimi opiniami i doświadczeniem w komentarzach.

Teraz chciałbym usłyszeć, co masz do powiedzenia:

Czego nauczyłeś się z dzisiejszego wpisu?

Co najbardziej Ciebie szokuje w tym jak błąd koniunkcji wpływa na nasze życie?

A może masz pytanie dotyczące czegoś z opisanych badań.

Tak czy inaczej, podziel się swoimi przemyśleniami w sekcji komentarzy poniżej.

• szkolenia online
• szkolenia u Ciebie w firmie i doradztwo-konsulting
• agencja SEO/SEM

Co myślisz o moim nowym wpisie na blogu?

A może masz pytanie dotyczące strategii lub techniki jak działać najlepiej?

Tak czy inaczej, chciałbym usłyszeć, co masz do powiedzenia.

Więc śmiało, teraz udostępnij ten wpis na swoich social mediach i zobacz co inni mają do powiedzenia.