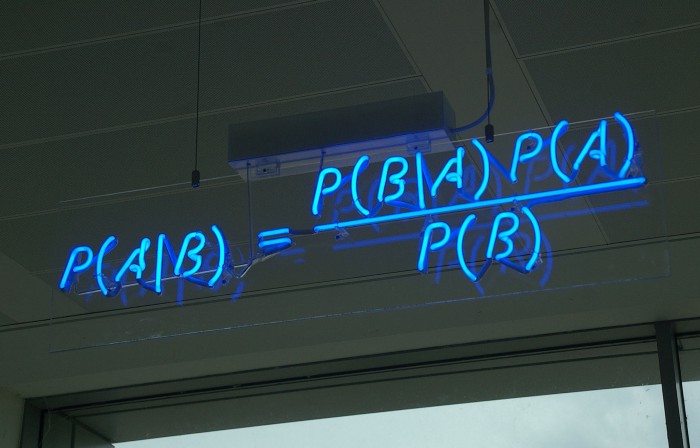
Co to jest twierdzenie Bayesa?

Twierdzenie Bayesa umożliwia nam aktualizację naszych przekonań w oparciu o pojawienie się nowych, odpowiednich dowodów.

Na przykład, gdybyśmy próbowali określić prawdopodobieństwo, że dana osoba ma raka, na początku powiedzielibyśmy, że jest to dowolny procent populacji, który ma raka.

Jednak biorąc pod uwagę dodatkowe dowody, takie jak fakt, że dana osoba jest palaczem, możemy zaktualizować nasze prawdopodobieństwo, ponieważ prawdopodobieństwo zachorowania na raka jest wyższe, biorąc pod uwagę, że dana osoba jest palaczem.

To pozwala nam wykorzystać wcześniejszą wiedzę do ulepszenia naszych oszacowań prawdopodobieństwa.

Prawdopodobieństwo całkowite wzór Bayesa

Pozwala nam poprawnie dostosować nasze przekonania do diagnostyki dowodów. Reguła Bayesa jest zgodna ze wzorem:

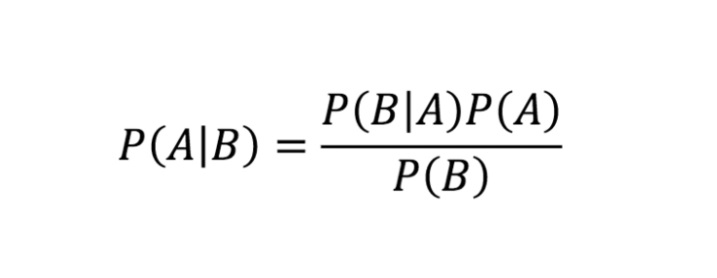
gdzie A i B są zdarzeniami oraz P(B)>0, przy czym:

• P(A|B) oznacza prawdopodobieństwo warunkowe, tj. prawdopodobieństwo zajścia zdarzenia A, o ile zajdzie zdarzenie B.
• P(B|A) oznacza prawdopodobieństwo zajścia zdarzenia B, o ile zajdzie zdarzenie A.

Zasadniczo wzór stwierdza, że ​​późniejsze szanse są proporcjonalne do poprzednich pomnożonych przez prawdopodobieństwo.

Poniżej rozwinięcie (dla chętnych, bardziej złożone):

Najpierw wyjaśnijmy 2 terminy.

Szanse a priori i szanse a posteriori

Twierdzenie Bayesa można wyrazić na wiele sposobów. Można to zrobić, korzystając z szans. Koncepcja ta zakłada przyjęcie szans, że coś się wydarzy (w przeciwieństwie do tego, że się nie wydarzy), które zapiszemy jako szanse a priori. Sformułowanie „a priori” odnosi się do naszej oceny szans przed uzyskaniem nowych informacji, które mogą być ważne. Celem tego wzoru jest uaktualnienie szans a priori po udostępnieniu nowych informacji i otrzymanie w ten sposób szans a posteriori lub szans po uzyskaniu informacji (według słownika „a posteriori” oznacza coś, co następuje po, później).

Reguła ma bardzo proste wyprowadzenie, które bezpośrednio wynika ze związku między prawdopodobieństwami łącznymi i warunkowymi. Po pierwsze, zauważ, że P (A, B) = P (A | B) P (B) = P (B, A) = P (B | A) P (A). Następnie możemy ustawić dwa wyrazy obejmujące prawdopodobieństwa warunkowe równe sobie, więc P (A | B) P (B) = P (B | A) P (A), a na koniec podziel obie strony przez P (B) dojść do reguły Bayesa.

W tym wzorze A jest zdarzeniem, którego prawdopodobieństwo jest pożądane, a B jest nowym dowodem, który jest w jakiś sposób powiązany z A.

P (A | B) nazywa się a priori. Rozkład a priori to rozkład parametrów przyjęty przed zaobserwowaniem jakichkolwiek danych, to właśnie próbujemy oszacować. W powyższym przykładzie byłoby to „prawdopodobieństwo zachorowania na raka, biorąc pod uwagę, że dana osoba jest palaczem”.

P (B | A) nazywa się prawdopodobieństwem; jest to prawdopodobieństwo zaobserwowania nowych dowodów, biorąc pod uwagę naszą wstępną hipotezę. W powyższym przykładzie byłoby to „prawdopodobieństwo bycia palaczem, biorąc pod uwagę, że dana osoba ma raka”.

P (A) nazywa się a posteriori. Rozkład a posteriori (in. wynikowy) to rozkład parametrów po uwzględnieniu zaobserwowanych danych. ; to jest prawdopodobieństwo naszej hipotezy bez żadnych wcześniejszych informacji. W powyższym przykładzie byłoby to „prawdopodobieństwo zachorowania na raka”.

P (B) nazywa się prawdopodobieństwem krańcowym. lub marginalnym; to jest całkowite prawdopodobieństwo zaobserwowania dowodów. W powyższym przykładzie byłoby to „prawdopodobieństwo bycia palaczem”. W wielu zastosowaniach reguły Bayesa jest to ignorowane, ponieważ służy głównie jako normalizacja.

Prawdopodobieństwo całkowite, a Twierdzenie Bayesa

Twierdzenie o prawdopodobieństwie całkowitym można zilustrować za pomocą drzewa stochastycznego.

Jeżeli zdarzenia B1,B2,…,Bn są parami rozłączne oraz mają prawdopodobieństwa dodatnie, które sumują się do jedynki, to dla dowolnego zdarzenia A zachodzi wzór:

P(A)=P(A|B1)⋅P(B1)+P(A|B2)⋅P(B2)+…+P(A|Bn)⋅P(Bn)

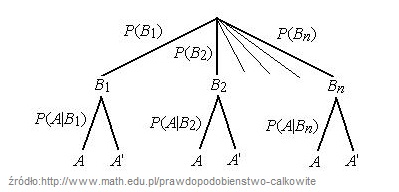
Wzór na prawdopodobieństwo całkowite to suma iloczynów po wszystkich drogach, które kończą się w A. Drzewo stochastyczne zaczyna się początkiem, w węzłach drzewa umieszczamy wyniki kolejnych etapów doświadczenia. Węzły łączymy krawędziami . Obok każdej krawędzi dopisujemy prawdopodobieństwo otrzymania wyniku danego etapu.

Suma prawdopodobieństw przyporządkowanych krawędziom wychodzącym z jednego węzła jest równa 1. Dowolny ciąg krawędzi łączący początek drzewa z jednym z końcowych węzłów nazywamy gałęzią drzewa. Każdej gałęzi odpowiada jeden wynik doświadczenia wieloetapowego. Prawdopodobieństwo wyniku odpowiadającego danej gałęzi drzewa równa się iloczynowi prawdopodobieństw przypisanych krawędziom, z których jest złożona gałąź (źródło).

REKLAMA

Koniecznie zobacz NAJLEPSZE szkolenie z Facebooka na rynku

Link do kursu: szkolenie Facebook Ads

Koniec reklamy.

Wnioskowanie bayesowskie (statystyka bayesowska) przykład

Korzystając z definicji z wikipedii:

Wnioskowanie bayesowskie (statystyka bayesowska) – metoda wnioskowania statystycznego, w której korzysta się z twierdzenia Bayesa do aktualizowania prawdopodobieństwa subiektywnego hipotez w oparciu o dotychczasowe prawdopodobieństwo oraz nowe dane. Wnioskowanie bayesowskie znajduje zastosowanie w wielu dziedzinach, takich jak badania naukowe, inżynieria, filozofia, medycyna, sport czy prawo.

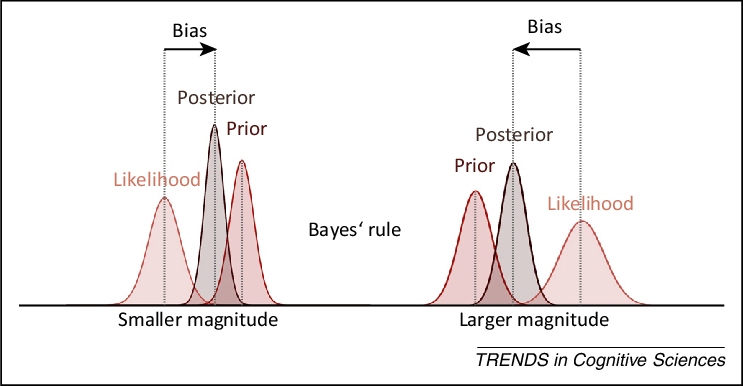
Poniżej jeszcze raz twierdzenie Bayesa, tym razem w wersji angielskiej jako grafika.

Twierdzenie Bayesa na przykładzie zawałów serca i nadwagi możemy pokazać, że reguła Bayesa pozwala nam uzyskać znacznie lepsze oszacowanie.

Teraz wstawimy do przykładu kilka zmyślonych liczb, abyśmy mogli ocenić różnicę, jaką spowodowało twierdzenie Bayesa. Załóżmy, że prawdopodobieństwo zawałów serca wynosi 0,05 – co oznacza, że ​​5% ludzi ma zawał serca.

Teraz załóżmy, że prawdopodobieństwo bycia otyłym wynosi 0,10 – co oznacza, że ​​10% osób jest otyłych, a 20% osób które przeszło zawał serca jest otyłych, więc P (zawał | otyłość) = 0,20.

Początkowo prawdopodobieństwo zawału jest po prostu bazowe, czyli 0,05.

Jednak korzystając z nowych dowodów, możemy zamiast tego obliczyć P (zawał | nadwaga), które jest równe (P ( zawał | nadwaga ) * P (zawał)) / P (nadwaga) = (0,20 * 0,05) / (0,10) = 0.10.

Wprowadzając nowe dowody, uzyskaliśmy zatem lepsze oszacowanie prawdopodobieństwa.

Początkowo mieliśmy prawdopodobieństwo 0,05, ale korzystając z dowodów dotyczących otyłości, byliśmy w stanie uzyskać dokładniejsze prawdopodobieństwo, które było dwukrotnie większe niż wcześniej. W podanym przykładzie (nawet z naszymi wymyślonymi liczbami) efekt ten powinien być całkiem logiczny, ponieważ wiemy, że otyłość powoduje zawały.

To pokazuje, jak reguła Bayesa pozwala nam aktualizować nasze przekonania przy użyciu odpowiednich informacji.

Wspomaganie decyzji, reguła Bayesa

Prawdziwą przydatność wnioskowania bayesowskiego można ocenić w zastosowaniach, z których najpopularniejszym jest wspomaganie decyzji(klasyfikacji).

Wspomaganie decyzji (klasyfikacji) jest szczególnym przykładem wykorzystania metod wnioskowań indukcyjnych takich jak predykcja, wnioskowanie przez analogię i indukcja eliminacyjna.

Statystycy i analitycy konstruują klasyfikatory bayesowskie, to jest algorytmy(procedury), które na podstawie próbki “nauczą się” wyznaczać prawdopodobieństwo wartości decyzji (klasyfikacji) dla nowych przykładów.

Ograniczenie wnioskowania do zadania klasyfikacji pozwala na uzyskanie efektywnych obliczeniowo metod jego automatyzacji.

Przechodząc na nieco wyższy poziom abstrakcji, możemy postawić wymaganie, by wybierana hipoteza nie tylko dobrze pasowała do rzeczywistości, ale była także jak najprostsza.

Jest to swoiste odwołanie do brzytwy Ockhama(lex parsimoniae).

Przyjmujemy najprostsze z możliwych wyjaśnienie, przy czym w ujęciu Williama z Ockham za najprostszą powinniśmy przyjmować hipotezę, która wymaga poczynienia najsłabszych (najmniej licznych) założeń.

W praktyce, szczególnie informatycznej, lex parsimoniae zastępuje się często zasadą najkrótszego (minimalnego) opisu (MDL – MinimumDescription Length).

MDL -Za najlepszą hipotezę uważamy taką, która prowadzi do najlepszej kompresji danych. To znaczy, ze przy przyjęcie tej hipotezy pozwala napisać możliwie najkrótszy/najprostszy algorytm odtwarzający dane.W przypadku klasyfikatorów, często oznacza to po prostu przyjęcie hipotezy o najkrótszym opisie

Wnioskowanie klasyczne, a wnioskowanie bayesowskie

W podejściu klasycznym wnioskowanie statystyczne oparte jest tylko na podstawie pobranej próby losowej. Możemy np. szacować punktowo, czy przedziałowo nieznane parametry rozkładów. Możemy także weryfikować hipotezy dotyczące rozkładów badanych cech. Ponadto możemy badać różne zależności pomiędzy badanymi cechami i wyznaczać dowolne praktycznie związki między nimi.

Na podstawie próby losowej wnioskujemy na temat całej badanej populacji.Stąd odpowiedni dobór próby jest obowiązkowy.

Prosty przykład, co by się stało gdyby koncerny samochodowe na nadchodzący rok wyprodukowały samochody w kolorach, ze źle dobranej próby ankietowej gdzie np. jako grupę wybrano głównie nastolatki? Mielibyśmy różowe BMW i mercedesy?

Także grupa do próby losowej musi być dobrana perfekcyjnie.

Oprócz podejścia klasycznego istnieje tzw. podejście bayesowskie, które pozwala analitykowi korzystać nie tylko z wyników zaobserwowanych w próbie, ale także z informacji a priori (wyjaśniliśmy ten termin wcześniej w tym wpisie) dotyczących rozważanego problemu.

W podejściu klasycznym zakładamy, że parametry rozkładu badanej cechy w populacji, takie jak średnia, wariancja, frakcja elementów określonego rodzaju w populacji są określonymi, choć nieznanymi wielkościami.

Natomiast w podejściu bayesowskim zakładamy, że interesujące nas parametry są zmiennymi losowymi.

Możemy zatem na podstawie wiedzy eksperckiej (informacji a priori) przewidywać ich rozkłady i na podstawie danych z próby modyfikować te założenia.

W podejściu bayesowskim matematyczny związek prawdopodobieństw wynikających z informacji a priori i prawdopodobieństw wynikających z obserwacji próby opiera się na twierdzeniu Bayesa i stąd jego nazwa.

Poniżej aby to przedstawić w prosty sposób grafika, podział podejścia bayesowskiego (wnioskowanie bayesowskie) i wnioskowanie klasyczne:

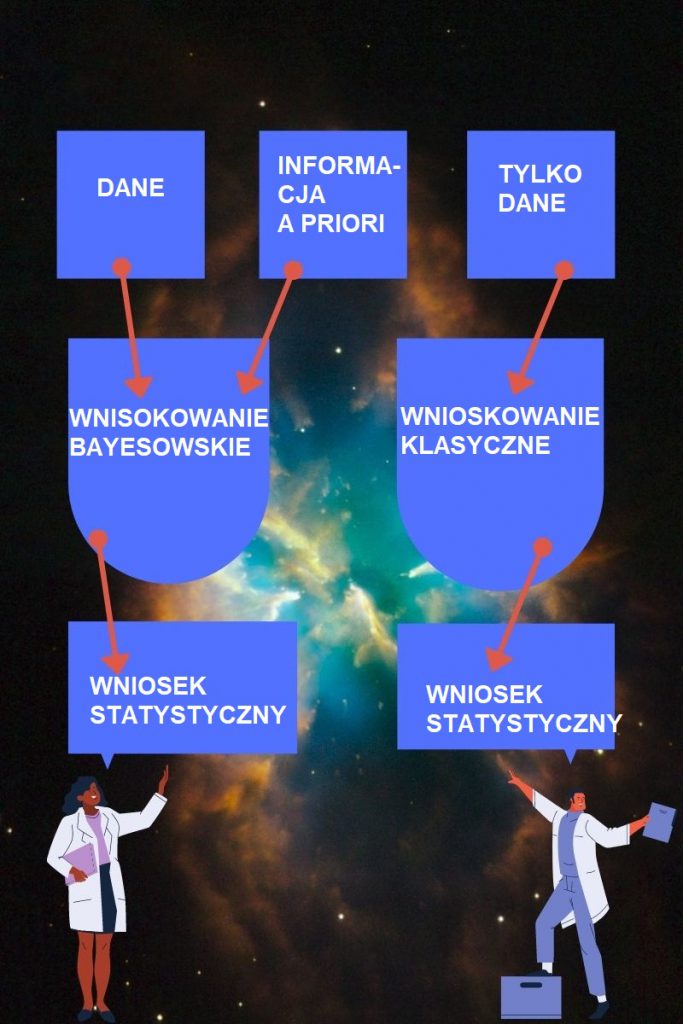
W ogólności podejście bayesowskie nie musi jednak doprowadzić do wniosków dokładniejszych niż podejście klasyczne. Jeżeli informacja a priori, którą dysponujemy jest dokładna, wówczas jej wykorzystanie łącznie z informacją pochodzącą z próby prowadzi do wniosków dokładniejszych od wniosków uzyskanych w podejściu klasycznym. Jeżeli jednak informacja a priori jest niedokładna, korzystanie z niej i z informacji z próby może prowadzić do wniosków mniej dokładnych od tych, do których doszlibyśmy pomijając informację a priori.

Jeżeli informacja a priori jest bezpośrednim rezultatem wcześniejszych badań statystycznych i nie opiera się na czyjejś przypadkowej wiedzy o badanym problemie, to analiza bayesowska jest w pełni obiektywna.

Często jednak informacja a priori odzwierciedla tylko osobiste poglądy osoby przeprowadzającej analizę lub innej osoby dysponującej tylko pewną przypadkową wiedzą o badanym problemie.

Wówczas informacja a priori ma charakter subiektywny i dlatego sama idea wykorzystania informacji a priori w analizie statystycznej jest często przez niektórych atakowana.

Zachęcam do podzielenia się swoimi opiniami i doświadczeniem w komentarzach.

Teraz chciałbym usłyszeć, co masz do powiedzenia:

Czego nauczyłeś się z dzisiejszego wpisu?

Co najbardziej Ciebie szokuje w tym jak twierdzenie Bayesa wpływa na nasze życie?

A może masz pytanie dotyczące czegoś z opisanych reguł.

Tak czy inaczej, podziel się swoimi przemyśleniami w sekcji komentarzy poniżej.

• szkolenia online
• szkolenia u Ciebie w firmie i doradztwo-konsulting
• agencja SEO/SEM

Co myślisz o moim nowym wpisie na blogu?

A może masz pytanie dotyczące strategii lub techniki jak działać najlepiej?

Tak czy inaczej, chciałbym usłyszeć, co masz do powiedzenia.

Więc śmiało, teraz udostępnij ten wpis na swoich social mediach i zobacz co inni mają do powiedzenia.